삽입 정렬
15 Oct 2018 | python sorting algorithm삽입 정렬이란?
정렬을 할 때, 자신보다 앞에 있는 배열들은 정렬이 되어있다고 가정하고 “자신의 위치를 찾아 삽입”하는 방법의 정렬이다. 즉 배열에서 정렬할 요소 선택하기 위해 모두 한번씩은 순회 해야하며(어떤 정렬이든 당연한 말이지만), 해당 요소를 선택한 경우에는 자신보다 앞에 있는 서브 배열을 순회하여 자신의 위치를 찾아야 한다. 즉, 처음부터 이쁘게 정렬이 되어있는 배열을 대상으로 삽입 정렬을 하려고 한다면 아주 빠르게(시간 복잡도 O(n)) 정렬이 가능하다.
과정

-
첫 번째 요소부터 배열을 순회하여 하나씩 정렬해 나간다. 따라서 가장 먼저 맨 첫번 째 요소를 선택한다.
그러나 첫 번쨰 요소의 경우 자신의 위치를 찾기위한 자기 앞의 정렬된 서브 배열이 없음으로 넘어간다. 그리고 이제 이 첫 번째 요소인 6은 정렬 된 서브 배열의 첫 구성원이 되었다.
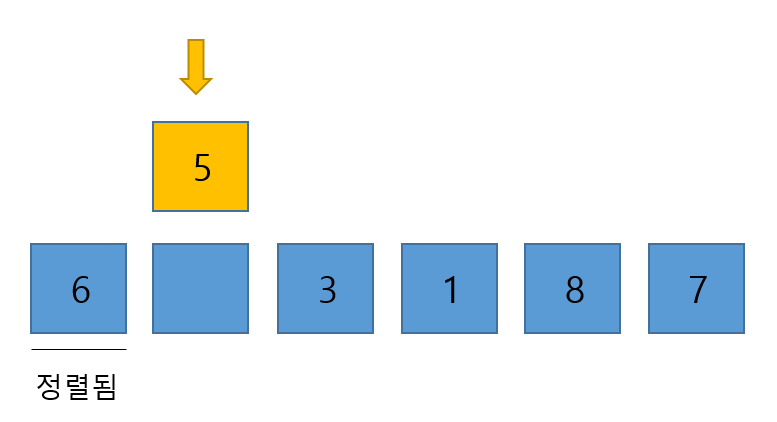
- 다음으로 5가 선택되었다.
선택된 5 앞에는 이미 정렬이 된 배열(그리고 우리가 꾸준히 정렬 해 나갈)이 존재하고 있다. 아직까진 정렬된 배열에 6 밖에 없다. 그럼, 5를 앞의 서브 배열의 어느 부분에 넣을지 생각해 보자.
- 일단 5를 빼내자. 서브 배열과 비교 도중 해당 요소인 5 보다 큰 요소가 한칸씩 밀려나가야 되기 때문에 이 빈 자리가 필요하다.
- 이제 이전에 빼낸 5와 서브 배열의 마지막 요소인 6과 비교한다. 6이 더 크기 때문에 6을 뒤로 한칸 밀어내고 5를 기존 6의 자리에 넣는다.
- 일단 5를 빼내자. 서브 배열과 비교 도중 해당 요소인 5 보다 큰 요소가 한칸씩 밀려나가야 되기 때문에 이 빈 자리가 필요하다.
- 다음은 3의 차례다. 3을 선택하고 빼내며 그 자리를 비워둔다(사실 비워두지 않아도 값은 덮어씌어 질 수 있어서 딱히 안비워도 되긴하다. 그러나 꼭 3을 따로 빼내야만 계속해서 3을 가지고 비교를 할 수 있다.).
- 빼낸 3을 이미 정렬된 앞의 서브 배열과 비교하며 적절한 위치에 삽입시킨다. 위의 과정과 동일하다.
여기서 눈여겨 볼 점은 이미 정렬된 서브 배열의 마지막 요소부터 비교하던지 첫 요소부터 비교하던지는 크게 중요하지 않다는 점이다! 하지만 상황에 따라 정 반대의 성능을 나타 낼 수가 있다. 왜일까? 만약 이미 오름 차순으로 정렬이 되어있는 요소를 그대로 오름 차순으로 정렬 할 경우, 우리가 하고 있는 방식(서브 배열의 마지막 요소부터 비교하는 방식)대로 라면 항상 서브 배열과 비교 하자마자 삽입될 위치가 정해진다. 예를 들어 1 2 3 4 5를 정렬 할 때, 3을 선택해서 삽입하려고 한다면, [1,2]로 된 서브배열에서 3의 위치를 찾아야 한다. [1,2]의 마지막 요소 2와 3을 비교하면 3이 크다. 한 번더, [1,2,3] 과 4의 관계도 마찬가지다. 처음 3과 4를 비교하면 바로 4의 위치가 나온다. 그렇다면 이번엔 5 4 3 2 1 로 구성된 요소를 오름차순으로 정렬해보자. 이때도 서브 배열의 마지막 요소부터 비교한다면 항상 끝까지 비교를 끝마쳐야 자신의 위치를 찾을 수 있다. 예를 들어 정렬이 완료된 서브 배열 [3,4,5]가 있고 이번 차례는 2라면, 5와 2를 비교, 4와 2를 비교, 3과 2를 비교해야만 자신의 위치가 가장 첫 자리로 배정된다. 이럴 땐 서브 배열의 첫 요소부터 비교하게끔 알고리즘을 작성하면 된다.
- 빼낸 3을 이미 정렬된 앞의 서브 배열과 비교하며 적절한 위치에 삽입시킨다. 위의 과정과 동일하다.
- 이후 과정인 1 8 7 을 정렬하는 과정은 같은 과정의 반복이므로 패스!
코드
def insertionSort(x):
for size in range(1, len(x)): # 삽입할 요소를 하나씩 선택하기 위한 루프
val = x[size]
i = size
while i > 0 and x[i-1] > val: # 정렬된 서브배열과 비교하는 루프
x[i] = x[i-1]
i -= 1
x[i] = val
시간복잡도
- 최선 : O(n)
- 평균 : O(n^2)
- 최악 : O(n^2)
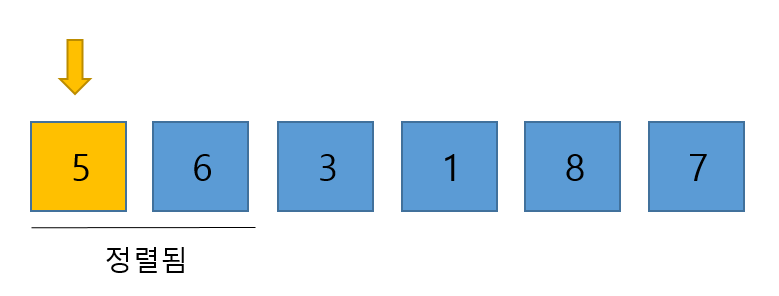
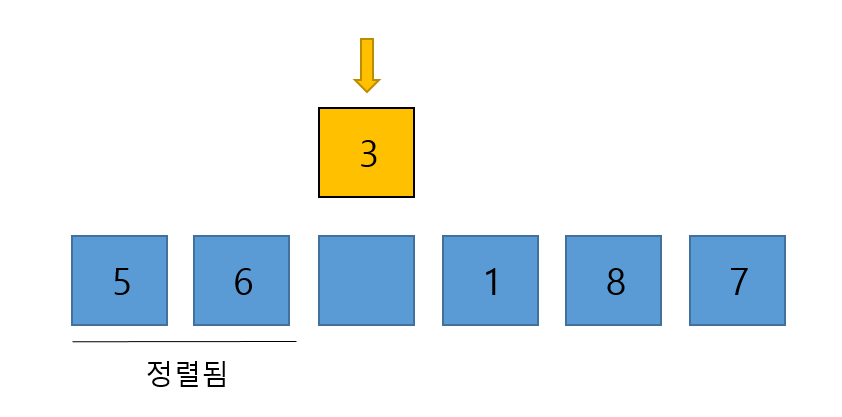
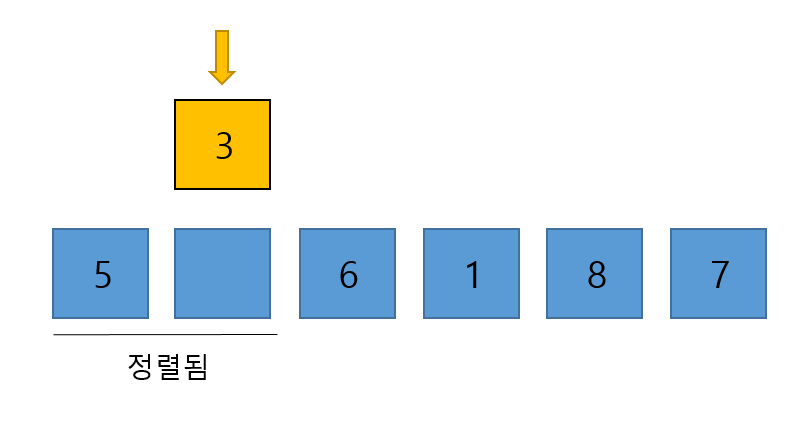
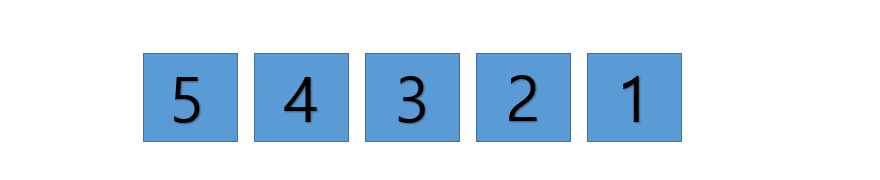

 (이렇게 되면 루프 한번에 한개의 요소가 정확히 정렬 된것이다. 제일 작은 것이 제일 왼쪽에 왔으니까!)
(이렇게 되면 루프 한번에 한개의 요소가 정확히 정렬 된것이다. 제일 작은 것이 제일 왼쪽에 왔으니까!)