백준 10451번 (순열사이클) with Java
04 Dec 2018 | algorithm java bfs graph문제
접근법
정답 비율이 60%가 넘을 만큼 간단하다. 그러나 이 문제는 주어진 숫자를 입력 받아서 그래프를 찾아내는 문제이기 때문에 그래프에 대한 이해와 bfs, 혹은 dfs에 대한 이해가 없으면 어려울 수도 있다.
문제 자체는 깔끔하고 이해하기가 쉽다. 문제를 다 읽고나면, 주어지는 숫자 하나하나의 인덱스와 주어진 값을 각각 노드로 생각해서 그 둘을 이어주면 될 것이라는 생각이 든다. 예를 들어 처음으로 3인 숫자가 들어왔다면, 인덱스가 1이니 노드1을 하나 만들어서 노드3를 향하게 하면된다. 이와 동일하게 두 번째로 2가 들어왔다. 이때 인덱스는 2다(두번째 값이니까). 따라서 노드2를 만들고, 방금 들어온 값인 노드2를 향하게 한다. 이 경우 노드2는 자기 자신을 가르키게 되는 그래프가 된다.
그래프는, 코드로 아래와 같이 구현하면 된다.
[
1 : [ 3 ],
2 : [ 2 ],
3 : [ 7 ],
4 : [ 8 ],
5 : [ 1 ],
6 : [ 4 ],
7 : [ 5 ],
8 : [ 6 ]
]
앞에 있는 key 값이 출발지 노드이고, value 배열 안에 들어있는 값들이 도착지 노드이다. 즉, 노드1은 노드3을 향하고, 노드3은 노드7을 향하는 것이다. 나는 개인적으로 이런 그래프 문제를 풀때 항상 노드를 class로 분리하는 것을 좋아하기 때문에, 별 내용은 없겠지만 Node 클래스를 만들었다.
이 노드는 자신이 향하고 있는 노드들을 child라는 리스트에 담을 것이다.
저런 그래프 관계를 구현하는건 단순한 작업이다.
이렇게 처음 빈 list에 입력 받은 n+1개의 크기만큼 노드를 생성한다. 이 노드에는 아직 어떤 child도 포함되어있지 않기 때문에 그냥 초기화라고 생각해도 된다. 이후 값을 하나씩 받아 들일 때 마다 그래프를 조금씩 채워나가는 것이다.
이제 1부터 N까지 모든 노드를 시작점으로 해서 bfs를 수행할 것이다. N개 만큼 bfs를 실행하는 것이다. 생각해보자, 1번 노드를 시작으로 bfs를 수행하면 1번 노드와 연결된 노드들 만이 선택(출력)될 것이다. 그말은 1번에서 시작된 bfs가 끝이난다면 그 순간 순열 사이클을 한개 찾은 것이다. 이제 2번 노드를 시작으로 bfs를 수행하자. 2번 역시 2번 노드와 연결된 노드들 만이 선택(출력)될 것이다. 3번도 마찬가지이다. 너무 간단하지않은가.
그런데 이 방법은 비효율적이다. 예시를 보아도 알겠지만 1번 노드에서 bfs를 시작하게 되면, 분명히 3번, 7번, 5번 노드를 거치게 된다. 즉, 3번 7번 5번 노드는 1번노드와 함께 같은 순열 사이클을 이루고 있다. 우리가 구하고자 하는 답은 순열 사이클의 갯수이기 때문에 3번 7번 5번을 시작으로 또 bfs를 돌 필요가 없다(5번에서 시작하나 1번에서 시작하나 결국 그것은 한개의 순열 사이클이기 때문).
3번 5번 7번 노드를 시작점으로 하는 bfs를 수행하지 않기 위해서 visited[] 배열을 사용하면 된다. 즉, 1번 노드를 시작으로 bfs를 돌면서 3,7,5번을 만날 때마다 3,7,5를 방문한 노드라고 표시해 두는 것이다.
글을 모두 읽었다면 아래 코드를 이해하는데 훨씬 수월할 것 같다.
import java.util.*;
public class B10451 {
final static Scanner scanner = new Scanner(System.in);
public static void main(String[] args) {
int testCase = scanner.nextInt();
for (int i = 0; i < testCase; i++) {
List<Node> list = new ArrayList<>();
int n = scanner.nextInt();
int[] visited = new int[n + 1];
Arrays.fill(visited, -1); // 방문한 노드는 1로 표기하자.
int answer = 0;
for (int k = 0; k < n + 1; k++) {
list.add(new Node());
}
for (int j = 1; j <= n; j++) {
int val = scanner.nextInt();
list.get(j).child.add(val);
}
for (int j = 1; j <= n; j++) {
// 이미 방문한 노드라면 bfs를 할 필요가 없다.
if (visited[j] == -1) {
answer += bfs(list, visited, j);
}
}
System.out.println(answer);
}
}
public static int bfs(List<Node> list, int [] visited, int start) {
Queue<Integer> q = new LinkedList<>();
q.offer(start);
visited[start] = 1;
while (!q.isEmpty()) {
int index = q.poll();
for (int val : list.get(index).child) {
if(visited[val] == -1) {
q.offer(val);
}
visited[val] = 1;
}
}
return 1;
}
static class Node {
List<Integer> child = new ArrayList<>();
}
}
아차!
이문제는 굳이 Node를 따로 빼낼 필요는 없다. 어차피 이 Node에는 ArrayList하나만 들어있으므로 그냥 ArrayList로 곧장 사용해도 된다. 이 문제는 그게 더 편할지도 모른다. 그러나 여러 문제를 풀다보면 이 문제처럼 Node가 간단한게 아니라 Node만이 가지는 특성들이 필요한 경우도 많기 때문에 Node를 빼냈다. 정답은 없다.
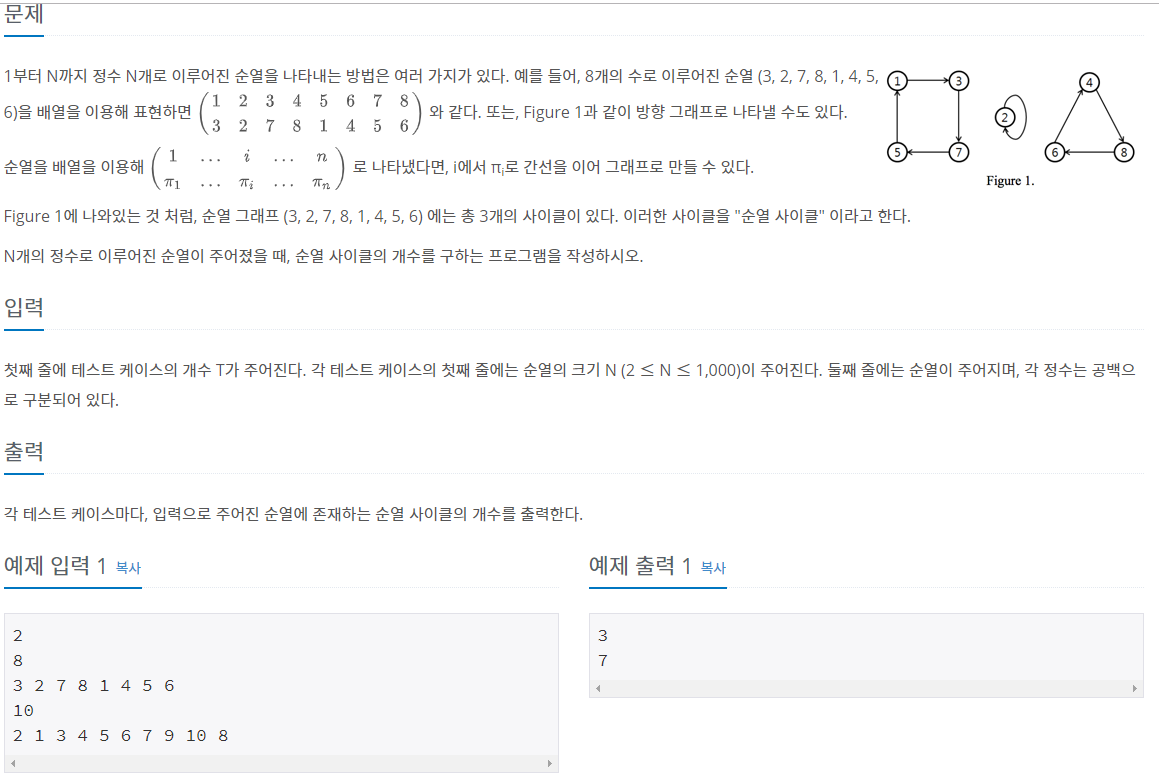
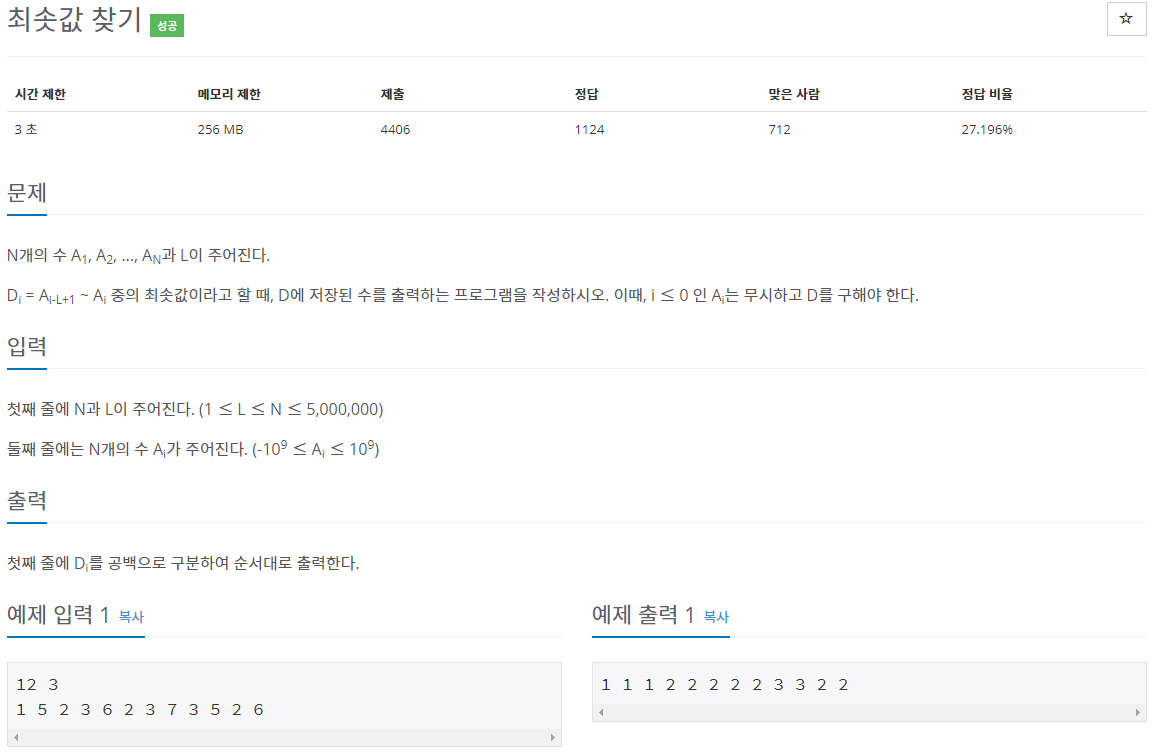
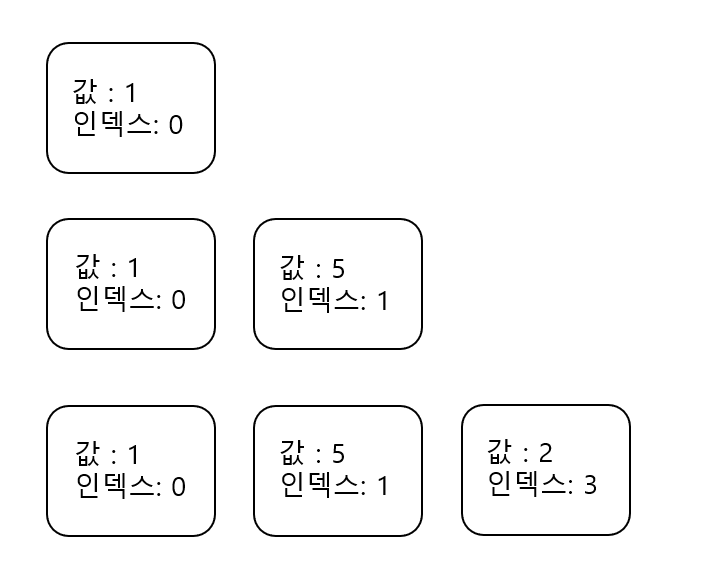
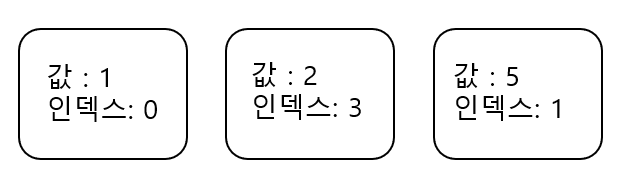
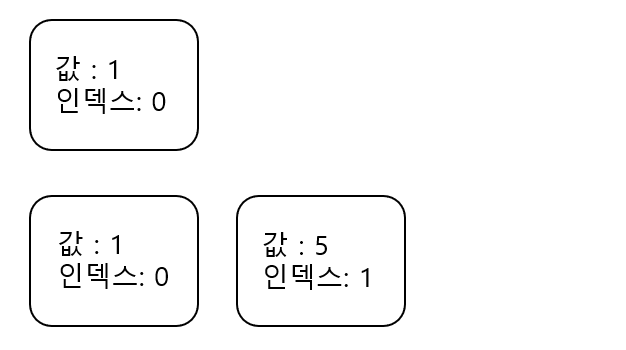현재 deque는 이 상황이다. 이제 {값:3, 인덱스:3} 인 박스가 들어올 것인데, 정렬을 하지 말고 차례대로 넣자. 대신 자신보다 값이 큰 값이 있다면 그 것을 pop해주고 자신을 넣자. 왜냐하면, 값이 5인 박스는 무조건 뒤에 들어올 값이 3인 박스보다 먼저 소멸된다. 즉, deque에 값1, 값5인 값 두개만 있다면 값: 1인 박스가 사라질 경우 최솟값이 값 : 5가 될 수 도 있겠지만, 값 5가 deque에 존재하는 상황에서 새로들어오는 박스의 값이 5보다 작다면 5는 절대 답이 될 수 없기 때문이다. 값 :5 인 박스가 아무리 지지고 볶아도 값:5인 박스와 값:3인 박스는 함께 deque에 존재한다(게다가 값:5의 인덱스가 빠르니까 값:5 박스가 먼저 사라진다).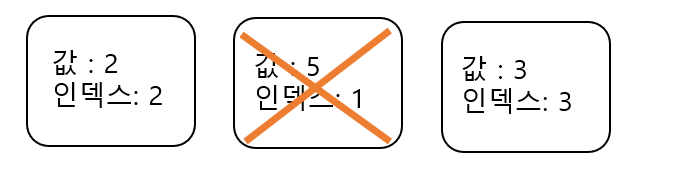
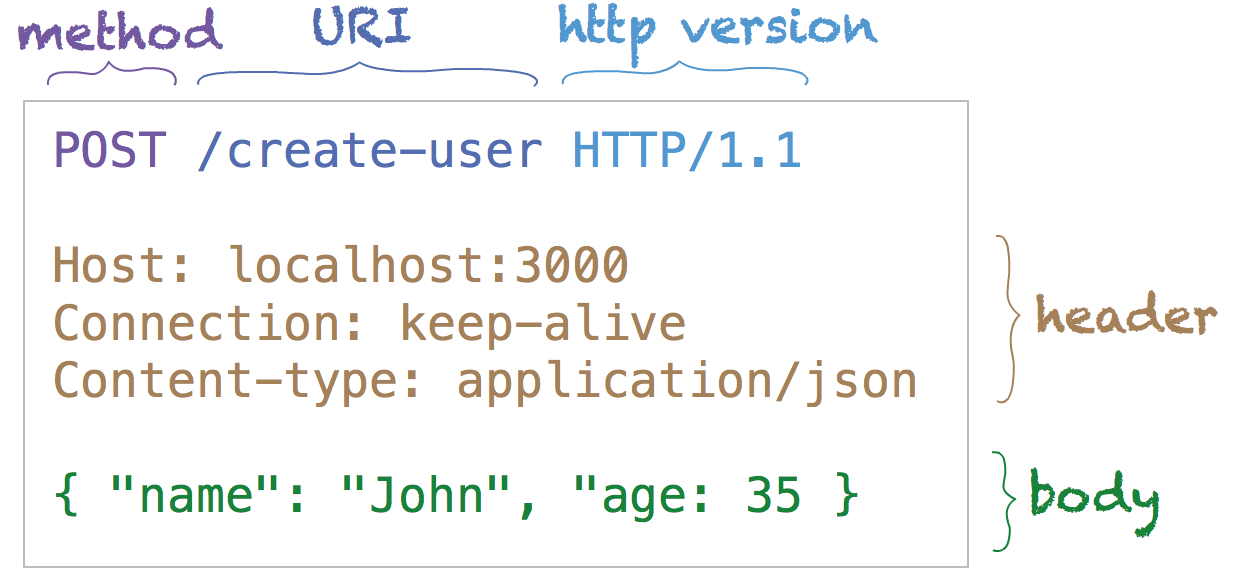위의 그림처럼 어떤 행위(get,post,delete,put 등등)를 할 것인지, uri가 무엇이고 http version이 몇인지, 그리고 부가적인 자세한 정보가 필요한 경우 Header값을 설정할 수 있다. 마지막으로 post와 같이 클라이언트에서 서버로 어떤 데이터를 전달 해야 할 경우 body영역에 데이터를 싣는다. 우리가 url을 입력하면 브라우저는 이를 해독해 그림과 같은 http 메세지를 자동으로 만들어 준다.