백준 2250번 문제 (트리의 높이와 너비) with Java
05 Dec 2018 | algorithm java Tree문제
이번 포스팅은 문제가 너무 길어서 링크만 걸어놓았다 ㅠㅠ.
이 사진만 보며 잘 생각해도 풀 수 있다. 문제 중간중간 계속 이 사진을 보며 푸는게 훨씬 효율적이고 생각 정리가 잘 되었다.
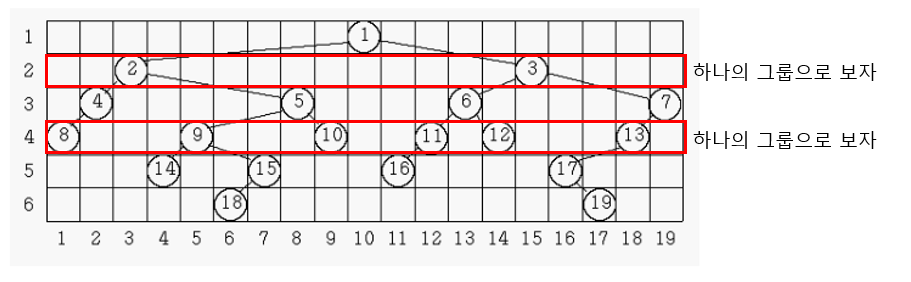
우리가 찾고자 하는 것은 같은 깊이(level)에 속해있는 노드들은 각각 하나의 집합으로 보고, 그 집합의 가장 왼쪽과, 가장 오른쪽 노드의 거리가 가장 먼 그룹의 깊이(level)와 그 너비를 출력하는 것이다. 즉, 위의 예제에서는 level3과 level4의 두 그룹이 너비 18을 가짐으로써 출력할 너비는 18이고, 레벨은 3과 4인데 더 작은 값인 3을 출력하면 된다.
접근법
우선 트리를 만드는 것은 당연하다. 당연한 말이지만 입력으로 들어오는 값을 바탕으로 트리를 만들고나서 어떤 아이디어로 푸느냐가 중요하다.
나같은 경우는 트리의 각 노드를 아래와 같은 클래스로 만들었다.
static class Node {
int parent; // 부모 번호
int num; // 자신의 번호
int left; // 왼쪽 노드 번호
int right; // 오른쪽 노드 번호
Node(int num, int left, int right) {
this.parent = -1;
this.num = num;
this.left = left;
this.right = right;
}
}
Node를 만들 때 우선 모든 parent를 -1로 설정한다. 이 것은 이 문제에 함정이 있기 때문이다. 이 문제에서 루트는 무조건 1부터 시작하지 않는다. 루트노드의 번호가 2,3 또는 100일 수도 있다는 것이다. 그래서 각 노드마다 parent를 -1로 초기화 해놓고, 실제 입력받는 값을 바탕으로 각 Node에 실질적 값을 할당 할 때, parent값을 바꿔줄 것이다. 그러면 나중에 root노드를 찾을 때 편하다. 모든 노드중에 parent가 변하지 않고 여전히 -1인 것을 찾으면, 그게 바로 루트 노드이기 때문이다.
그리고 필요한 것은 각 레벨(깊이)그룹마다 제일 왼쪽에 있는 값의 x좌표 값과, 제일 오른쪽에 있는 값의 x좌표 값이다.
위의 그림을 예로 들면 level2의 가장 왼쪽 좌표는 3이고, 가장 오른쪽 좌표는 15니까 너비(width)는 15-3+1이다. 즉, 모든 레벨마다 너비(width)를 구하고 그 중 가장 넓은 값을 출력할 것이기 때문에 각 level마다 좌표의 최소, 최댓값을 저장해야 한다. 그 값들은 아래의 변수에 저장할 것이다.
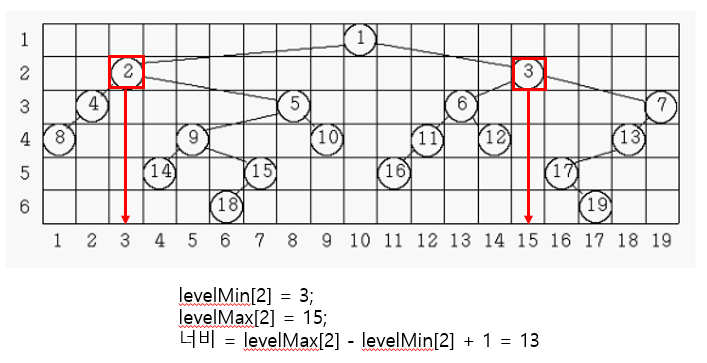
static int[] levelMin;
static int[] levelMax;
결국 우리는 트리를 천천히 순회하면서 각 레벨의 최소 x좌표, 최대 x좌표 값만 찾으면 된다.
트리를 순회하면서 levelMin, levelMax에 값을 넣어보자.
트리에는 세가지 방법의 순회가 있다.
- 전위 순회 (루트 -> 왼쪽 -> 오른쪽)
- 중위 순회 (왼쪽 -> 루트 -> 오른쪽)
- 후위 순회 (왼쪽 -> 오른쪽 -> 루트)
이 세가지 방법 중에 하나로 트리를 순회해야 하는데 어떤 방법으로 순회하는게 알맞아 보이는가?
중위 순회가 알맞다! 왜냐하면 우리는 트리를 순회하며 모든 노드들을 방문 할 것인데, 중위 순회의 경우는 가장 먼저 방문하는 노드가 가장 왼쪽 노드이기 때문이다. 가장 먼저 방문한 노드의 좌표를 1로 설정한다면 두 번째 방문하게 되는 노드는? 좌표가 2일 것이다. 중위 순회를 하면 방문하는 순서 그대로가 각 노드의 x좌표가 된다!
예시 사진을 보면, 중위 순회로 인해 가장 먼저 방문하는 노드는 8이고, 이를 x좌표 1로 설정한다. 그 다음 방문은 4이며 x좌표는 아까의 좌표에서 1높게 설정하면 그만이다. 이 부분 때문에 제일 윗 부분에서 사진을 보고 문제를 푸는것이 효율적이었다고 말한 것이다.
결국 우리는 중위순회를 하면서 그 노드가 level이 몇이고, 현재 이 노드의 x좌표 값이 같은 레벨에서 가장 왼쪽 값인지, 가장 오른쪽 값인지만 판단하면 되는 것이다. 그리고 가장 왼쪽 값이거나 가장 오른쪽 값이라면? 위에서 선언했던 levelMin[] 배열 또는 levelMax[]을 갱신해주면 된다.
이게 전부다. 이제 전체 코드를 보면서 쉽게 이해할 수 있을 것이다.
import java.util.ArrayList;
import java.util.List;
import java.util.Scanner;
public class B2250 {
final static Scanner scanner = new Scanner(System.in);
// point : 현재 x좌표 (노드를 방문할 때 마다 +1 증가)
static int point = 1;
static List<Node> tree = new ArrayList<>();
static int[] levelMin;
static int[] levelMax;
static int maxLevel = 0; // 트리의 최대 레벨(깊이)
public static void main(String[] args) {
int n = scanner.nextInt();
levelMin = new int[n+1];
levelMax = new int[n+1];
int rootIndex = 0;
for(int i =0; i<=n; i++) {
tree.add(new Node(i, -1, -1));
levelMin[i] = n;
levelMax[i] = 0;
}
for(int i = 0; i < n; i++) {
int num = scanner.nextInt();
int left = scanner.nextInt();
int right = scanner.nextInt();
tree.get(num).left = left;
tree.get(num).right = right;
if(left != -1) tree.get(left).parent = num;
if(right != -1) tree.get(right).parent = num;
}
for(int i = 1; i<=n; i++) {
if(tree.get(i).parent == -1) {
rootIndex = i;
break;
}
}
inOrder(rootIndex, 1);
// 완성된 levelMax[]와 levelMin[]을 가지고 값을 뽑아내기
int answerLevel = 1;
int answerWidth = levelMax[1] - levelMin[1] + 1;
for (int i = 2; i<= maxLevel; i++) {
int width = levelMax[i] - levelMin[i] + 1;
if(answerWidth < width) {
answerLevel = i;
answerWidth = width;
}
}
System.out.println(answerLevel + " " + answerWidth);
}
public static void inOrder(int rootIndex, int level) {
Node root = tree.get(rootIndex);
if(maxLevel < level) maxLevel = level;
if(root.left != -1) {
inOrder(root.left, level + 1);
}
// 현재 노드가 가장 왼쪽 노드라면 갱신
levelMin[level] = Math.min(levelMin[level], point);
// 현재 노드는 이전노드보다 항상 x좌표가 더 높기 때문에 갱신
levelMax[level] = point;
point++;
if(root.right != -1) {
inOrder(root.right, level + 1);
}
}
static class Node {
int parent;
int num;
int left;
int right;
Node(int num, int left, int right) {
this.parent = -1;
this.num = num;
this.left = left;
this.right = right;
}
}
}
아차!
static List<Node> tree = new ArrayList<>();
이 부분은 그냥 배열로 해도 됐었는데…
Comments